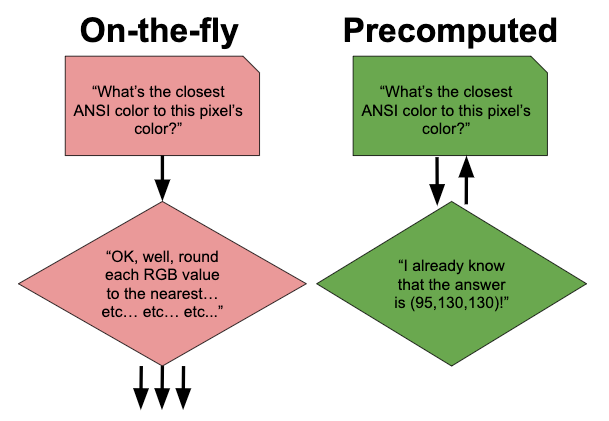
Last time on Programming Feedback for Advanced Beginners we wrote a program that used pre-computation to speed up Justin Reppert's ASCII art program. We calculated the closest ANSI color for every possible pixel color, and stored the answers in a file. Whenever we ran our ASCII art-generating program, we first loaded our previous pre-computations back into a color map, and then used them to find the best ANSI color for each pixel color almost instantly.
When I was writing the code for that edition of PFAB, my precomputed file was over 100MB in size and took around 30 seconds to load whenever I ran the program. This wasn't a big problem, but while I was waiting I started daydreaming. If we tried, how small could we make this file? And since smaller files are quicker for a program to read, how much time would doing this save us? This (and next) time on PFAB, we're going to find out.
We'll learn a lot about serialization, hexadecimal and problem solving. None of what follows is necessarily the best way to do anything, and I'm sure I've glossed over lots of micro-optimizations. However, it should still help you think more deeply about how computers work.
If you haven't read the previous two editions of PFAB then I'd suggest starting with them (#16, #17). Then let's begin today's edition by learning a long word for a simple concept.
In order to re-use our pre-computed color map, we'll need to write its contents to a file. When we want to use our color map again, we'll read the file back into our program and use the information inside it re-create our original map. In order to do this, we'll need to a set of rules for converting the data in our program into a long string that can be written to a file. We'll also need a corresponding set of rules converting that long string back into our color map data. These rules are called a serialization format.
Some common, generic serialization formats that you may or may not have heard of include JSON, YAML, Pickle, and XML. As we'll see, we can also define our own, specialized serialization formats that are only ever used by our program. A serialization format is just a pair of rules for writing and reading data - there's nothing stopping you from making up your own rules.
The process of turning data into something (specifically, a stream of bytes) that can be written to a file is called serialization, and the opposite process of turning a file back into data inside a program is called deserialization. The same de/serialization processes can also be used when sending and receiving data over a network (like the internet).
+------------+ Serialization +-----------------+
| +---------------->| Bytes that |
| Data in | | can be saved |
| a program | | to file/sent |
| +<----------------+ over network/etc|
+------------+ Deserialization +-----------------+
The simplest way to serialize our color mapping is to use a pre-existing, general-purpose serialization format like JSON. We'll soon go off in some strange directions in our quest for compactness, but JSON is where we'll start.
A JSON string looks something like this:
{
"key": "value",
"another_key": {
"nested_key": [1,2,3],
"another_nested_key": [4,5,6]
}
}
We used JSON in our first version of this program from the previous edition, which was a very sensible and pragmatic approach. If I hadn't already decided that I wanted this week's PFAB to go into unnecessary detail about file minification then I'd say that we should use JSON and call it a day. Every language has at least one well-tested library for writing JSON to files and reading it back out into structured data. JSON is even straightforward for humans to read, which helps with debugging. But flexibility and readability come at the cost of verbosity, and for today verbosity is the enemy.
Nonetheless, the first version of my precomputation code stored its data in a file of "pretty" JSON. "Pretty" JSON means that each new element is written on a new line and is indented to make it clearer to see where blocks begin and end. My file looked something like this:
{
"(0,0,0)": 0,
"(0,0,0)": 1,
// ...etc...
"(175,135,255)": 141,
// ...etc...
}
Let's estimate how large a pretty JSON color map will be. This will allow us to compare its size to that of the more compact approaches we'll soon look at.
If we look at the example JSON color map above, we can see that each pixel color/ANSI pair requires between 18 and 26 characters to store, depending on how many digits there were in each number. In a file (or indeed any string) a line break is represented by a \n character, which added an extra character per line.
Let's assume that 1 character requires 1 byte of storage in a file. The exact value actually depends on a file's character encoding - the way in which a series of bits and bytes on your hard drive are converted into meaningful strings. Common examples of character encodings are ASCII and UTF-8. Character encodings can be fiddly and frustrating, and since you don't need to know anything about them for this post we won't discuss them any further.
Let's stick with the assumption that 1 character takes up 1 byte. There are 256*256*256 = 16.7 million different pixel color/ANSI pairs that we need to store, so we would expect a pretty JSON file representing them to be around 16.7 million colors * 26 bytes/color = 434 million bytes = 434MB in size. A photo taken by your smartphone is about 1-2MB, so 434MB is quite a weight. Let's look at how we can use different serialization formats to make it smaller.
We can shrink our file by condensing the JSON inside it without fundamentally changing its meaning. Our program doesn't care how pretty or ugly our JSON is as long as it's valid. This means that we can immediately save some bytes by turning off pretty-mode. This gets rid of all extraneous newlines and whitespace and prints the entire JSON object on a single line:
{"(0,0,0)":0,"(0,0,1)":0,...etc...}
We can save a few more characters by noticing that we don't strictly need the brackets in the keys (i.e. the ( and ) in the "(0,0,0)"). The reason I've kept these brackets up until now is that they allow us to use a convenient if fragile hack for quickly looking up pixel colors in Python.
In order to look up the ANSI color for a pixel color tuple (eg. (0,0,0)), we need to have a standard process for turning that tuple into a string key that we can look up in our color map. Passing a tuple into the str function (i.e. calling str((0,0,0,))) returns a string of the elements of the tuple, surrounded by brackets (i.e. the string "(0,0,0)"). Using this output as the key in our color map means that in Python we can convert a tuple to a key simply by using the str function.
As we've discussed, we can shorten these keys by removing the brackets from them. This will mean that we need to write a little more code in order to turn a pixel tuple into a key, since we can no longer rely on simply the str function. This is no bad thing, since having our program implicitly depend on the way in which Python happens to convert tuples to strings makes for fragile, hard-to-follow code. Making this change will give us an ugly JSON file that looks like this:
{"0,0,0":0,"0,0,1":0,...etc...}
Now each extra pixel pair takes up between 10 and 18 characters, a saving of around 33% over pretty JSON. This is progress. We could keep trying to squeeze our JSON further and further, but I think that now is a prudent time for us to explore creating a custom serialization format.
As we've discussed already, JSON is a very flexible way to serialize data. It can handle strings, integers, booleans, lists, and maps, all nested as deep as your use-case requires. This flexibility is why JSON is so widely used. However, with great flexibility comes extra verbosity in the form of commas, colons, and square- and curly-brackets. Our use-case is very specific and well-defined and so doesn't need any flexibility. We can therefore invent and use our own specialized serialization format, safely sacrificing some versatility in exchange for terser output. This means that we have to decide on our own form for representing a color map in a file, as well as writing our own code to convert our precomputed data to and from this form.
Inventing a custom serialization format in order to save a few bytes is rarely a good idea. It's almost always worth accepting slightly bloated output in return for flexibility, readability, and standardization. But, for better or for worse, today we've decided that the only thing we care about is pure resource efficiency. Let's therefore see how we can sacrifice some of these boons in exchange for further space savings. For our first attempt at a serialization format, let's use the following rules:
Each color pair is on a new line
The first part of the line is the pixel color, in RGB form. Each RGB element should be separated by a comma
This should be followed by a pipe (|)
Then the final part of the line is the ANSI color ID
For example:
0,0,0|0
0,0,1|0
// ...etc..
175,135,255|141
// ...etc..
Now each pixel pair takes up between 8 and 16 characters, depending on the length of the numbers (don't forget the newline \n character). The main savings over our ugly JSON have come from removing the need for speech-marks around each key (eg. "0,0,0":0 has become 0,0,0|0). This is further progress, but we can still keep going.
Each line still contains 4 "information-less" characters: the 2 commas, 1 pipe, and 1 newline. These characters' only purpose is to indicate that one number has finished and the next number has started. Their relative lack of importance suggests that we might be able to get rid of them, but doing so is not straightforward. Each RGB number and ANSI ID can be either 1, 2, or 3 digits long, and so if we simply removed the commas and pipes then many lines would become ambiguous. For example, how should we parse this line?
92255182
There's no way for us to know whether this represents 92,25,51|82, or 9,225,5|182, or any one of many other ways of dividing up the digits. We could solve this problem by requiring that every number written using exactly 3 digits, adding leading padding with zeroes where necessary. This would alter numbers like so:
7 => 007
45 => 045
112 => 112
This would allow us to confidently treat every fixed-width block of 3 digits as a new number, removing the need for any separators. For example, this line:
092255001082
can be unambiguously parsed as 92,255,1|82. However, since nearly half the numbers in the range 0-255 have only 1 or 2 digits (i.e. all numbers from 0-99), we would end up having to add a lot of leading 0s for padding. We'd have removed all the commas and pipes, but replaced them with 0s instead, undoing a lot of our gains.
We can adapt this approach by continuing to use fixed-width values for our numbers, but this time using the hexadecimal counting system. Hexadecimal (often shortened to "hex") is an alternative to the standard, decimal system of representing numbers. It uses the digits 0-9 to represent the decimal numbers 0-9, but then also uses the letters A-F to represent the decimal numbers 10-15. To count to the decimal number 20 in hex, you go 1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,10,11,12,13,14. For more on hex, see this article.
Conveniently, every decimal number between 0 and 255 can be represented as a hex number with only 1 or 2 digits. The decimal number 0 is also 0 in hex, and decimal 255 is FF in hex. This means that we can write our previous, separator-less line using padded hex numbers as:
5CFF0152
We've still got rid of all the commas and pipes, but by using hex instead of decimal numbers we've drastically reduced the character length and the amount of 0-padding that we need. Since we know that every line will be exactly 8 characters long (6 for the pixel color, 2 for the ANSI ID), we don't even need the new line characters (\n) anymore. We can instead put all of our data on a single line, and confidently break it up into color pair blocks every 8 characters.
We're now down to exactly 8 bytes for every color pair, a saving of around 75% on the 18-26 required by our original pretty JSON. Of course, we can still do even better. But we've learned enough about serialization, files, and numbering systems for one week, so we'll finish off this problem next time on Programming Feedback for Advanced Beginners.
More posts from my blog: